The Mathematics of English

When you spend a lot of time constructing word-based puzzles, a mathematics of letters emerges. The most basic example is word length. Let's build a toolkit of more advanced mathematics and use it to gain an appreciation for different puzzles. For brevity, the term dataset refers to a specific collection of letters or words.

Patterns

Before we even think about numerical tools, we should be prepared to see words as patterns. Words beginning with the letter H (Her Happy Horses); words with three sets of doubled letters (Addressee, Bookkeeper); palindromes (Deed, Redder, Deified); and so on. Patterns are the basis for many word puzzles and games. Here is a fun website to explore:

Enumerated Patterns of Repetition

This is a programming tool, which turns a word into a number, based on the presence of repeated letters. SIMPLE becomes 123456, while PIMPLE becomes 123156 and CROSSFIRE becomes 123446729. These numbers can be grouped together to find interesting similarities. Their real power comes when they are combined with other tools and puzzle ideas.

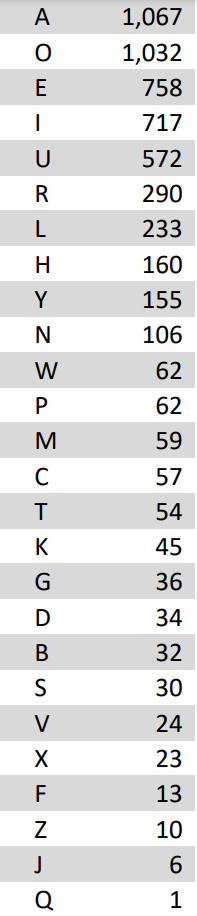
Letter Frequency

Different languages have different relative letter frequencies. Knowing the frequency of letters in English words, we can create balanced datasets for Boggle cubes, Boggle grids and word games like Scrabble. In English text, E is the most frequently used letter, followed by T, A, O, I, N, S, H, R, L, D, U. This sequence is immortalized in popular culture.

One use I have for letter frequency in puzzle design involves filtering words into tiny datasets and then sorting those datasets by how many members are in each. For example, how many four-letter words share the same second letter?

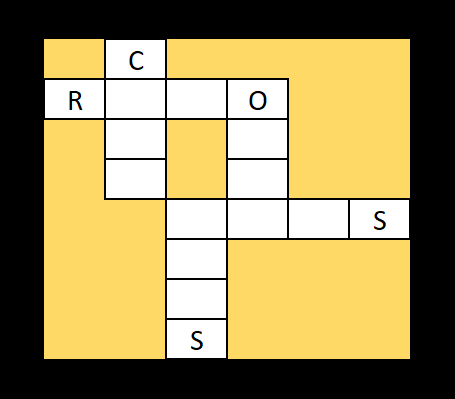
Armed with this information, I can create a puzzle based on intersecting words. Here is a little grid, pre-filled with clue letters:

I have two construction choices. I could provide a list of words and ask you to figure out which ones fit, but that is too much like a Fill-in or Kriss-Kross. The other option is to ask you to fill in the grid with five four-letter words. Let's do that!

First of all, I have to ensure that at least one solution exists. Using my frequency chart, I can focus on words that fit the patterns Cx?? and Rx?O. The question marks are place holders for any letters, while the little x is a placeholder for a common letter. My job as the constructor is to find x. You can probably see at least one suitable pair.

Having ascertained that Cx?? and Rx?? have solutions, I need to check for the next intersecting pair: O??x and ?x?S. At first glance, there appear to be many solutions. However, the final intersection, two words ending in S, restrict the possibilities of ?x?S in that second intersection! Thankfully, English is bursting with suitable candidates:

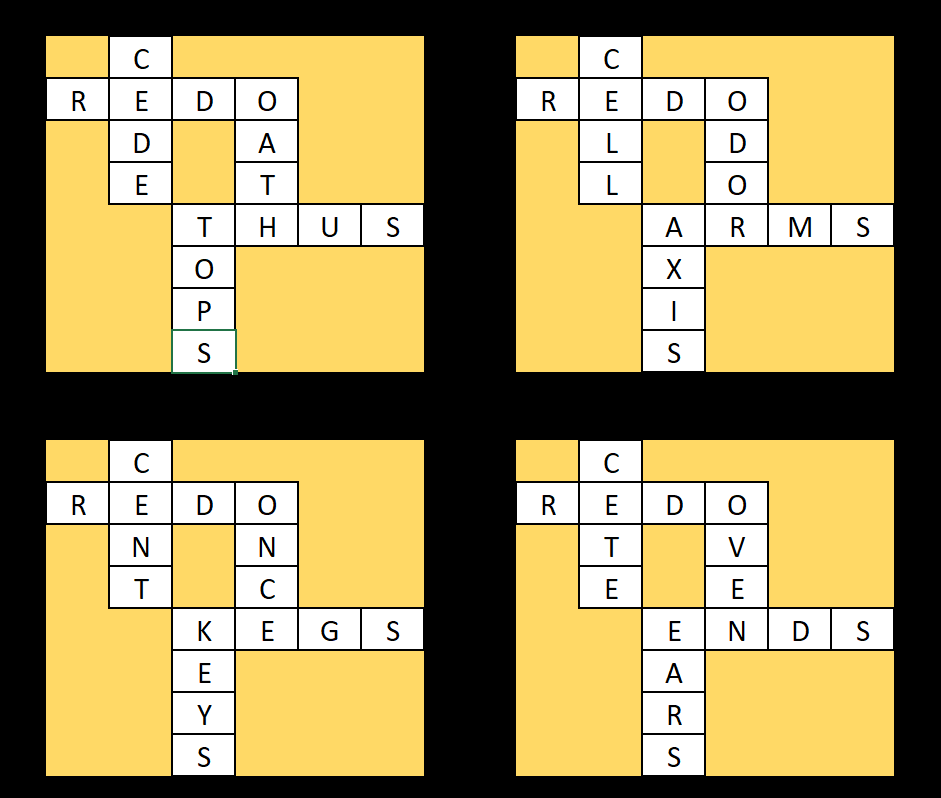
That may be a bit too easy. What if I were to constrain the grid? I could give you a list of letters that must be placed into the grid (still a bit Kriss-Krossy, but more challenging):

Or I could seed the grid with letters further down the frequency list, say fewer than 50 words per dataset?

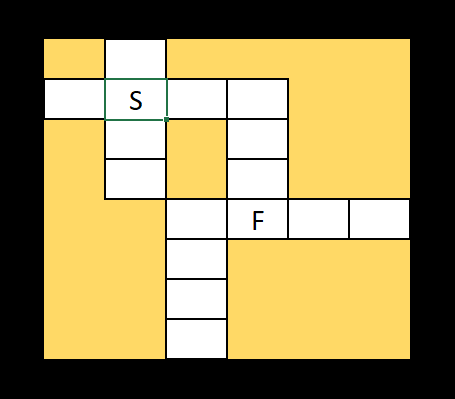
One thing I like about this puzzle is that its small size hides its complexity. I want the solver to have the satisfaction of finding just the right words that will fill the grid.

Patterns are useful for comparing words. For cryptogram lovers, frequencies are a fair starting point; however, most cryptograms are too short for frequencies to hold with statistical relevance. Solving cryptograms strategically requires that you recognize certain patterns, such as XYZX. How many four letter words begin and end with the same letter and have two different letters in the middle? My database returns a whopping 173!

In the context of cryptograms, we are not looking for obscure words (crosswordese), but familiar words like DIED, EASE, EDGE, GANG, HATH, HIGH, ONTO, POMP, PROP, PUMP, SAYS, SETS, SINS, SITS, SONS, SOWS, SUMS and THAT.

Of those, the most common is THAT. If you also find XY?, you can be almost certain that the three-letter word is THE and the four letter-word is THAT, even if the three-letter word turns out to be THY!

Other patterns involve suffixes like ING. If you see two coded words, such as QPXW and QPXWXYZ, maybe XYZ is ING. A less common ending would be IER.

Finally, by combining frequencies with patterns and the strength of your vocabulary, you can begin to crack cryptograms with ease. Simple words are easier to crack, once you get a larger word. Conversely, larger words are constrained by the possibilities for smaller words.

Alphagrams

After playing around with patterns and frequencies, we're ready to add another tool. If you sort the letters of a word alphabetically, the sorted letters are that word's alphagram. Alphagrams are handy for finding all anagrams of a particular word. For example, AELPT is the alphagram for eight words: LEAPT, LEPTA, PALET, PELTA, PETAL, PLATE, PLEAT and TEPAL. Depending on the type of puzzle I want to construct, I'll exclude all crosswordese or give solvers a pat on the back for knowing the plural of a monetary unit of Greece.

Alphagrams, while powerful on their own, need to be combined with other puzzle ideas in order to clamber from the anagram swamp. I use alphagrams for inspiration, such as: how many different six-letter words can be made by adding a single letter to PLATE and rearranging the six letters? Use each letter of the alphabet no more than once. So, PLATES and PETALS count as one answer. (Send your answers in the comments!)

Here is a final example: remember the enumerated patterns of repetition? Combine 123456789 with a length of nine and you have all the candidate words for a puzzle known as Wordoku (Sudoku with letters instead of numbers.) While most such puzzles use a random selection of nine different letters, I like to create the puzzle from nine-letter words and then make a theme. You can check out the attached PDF for some that I created.

Metamathematics

This final tool is a bit of language arts, combined with probabilities. As such, I have no strict definition of it. Essentially, it is the belief that there are enough words in the English language to satisfy any arbitrary set of constraints (within reason, of course.) I mentioned this before (scroll to Molding Something New, where I talk about the Pyramid Scheme puzzle) and it empowers my creativity to know that, lurking in my database, is that one word which completes the whole puzzle. Indeed, I very rarely need to abandon a puzzle for want of a word. When I created the little C-R-O-S-S grid, I pre-filled those five letters for thematic purposes, confident that enough words existed to create at least one solution.

So, what might be an interesting set of constraints? If you have Mind-bending variety Puzzles Volume 1, check out Match Wits, on page 38 and 3 x 15 = 15, on page 79. Both puzzles consist of long words made up of shorter words.

In Match Wits, a ten-letter word can be made from a four- and a six-letter word, where both smaller words begin with the same letter. So that puzzle has three length constraints and one pattern constraint.

3 x 5 = 15 consists of four puzzles. In each, a 15-letter word can be made from the letters in five three-letter word clues. The word is suggested by the title of the puzzle and the image. Additionally, three five-letter words can be made from the same 15 letters. The first letter of each five-letter word is given as a final constraint (without which, any old five-letter words would do.) So, these have three length constraints and one pattern constraint.

Scenario setting is important for differentiating words-within-words puzzles. Match Wits has crossword-style clues, while 3 x 5 = 15 relies on visual clues and prompts (the 3-letter words and the initial letters.)

Summary

Imbuing the words of English with numerical properties provides a massive foundation for creating all sorts of word-based puzzles. As a programmer, I leverage Excel's number-crunching power to mine my database of words, excavating fascinating combinations that would take forever to find on my own.